Skip to main content

Section 6.1 Discrete Random Variables

Definition 6.1.1.

A random variable is a numerical measure of a probability experiment, so its value is determined by chance. Random variables are typically denoted by capital letters such as \(X\) or \(Y\text{.}\)

Definition 6.1.2.

A discrete random variable has either a finite or countable number of values.

A continuous random variables has infinitely many values.

Definition 6.1.3. Probability Distributions.

The probability distribution of a discrete random variable \(X\) provides the possible values of the random variable and their corresponding probabilities. A probability distribution can be in the form of a table, graph, or mathematical formula.

  1. \(\sum P(x) = 1\)
  2. \(0 \le P(x) \le 1\)
Example 6.1.5. Mean Number of People in Household.

The formula for computing the mean of a discrete random variable is equivalent to how we compute the average. For example, a small class of statistics students was asked how many people live in their households. The following data was obtained:

\begin{equation*} 2, 4, 6, 6, 4, 4, 2, 3, 5, 5 \end{equation*}

What is the mean or average number of people per household?

\begin{align*} \mu \amp = \frac{\sum x_i}{N} = \frac{2+4+6+6+4+4+2+3+5+5}{10}\\ \amp = \frac{ \overbrace{2 + 2}^{2} + \overbrace{3}^{1} + \overbrace{4 + 4 + 4}^{3} + \overbrace{5 + 5}^{2} + \overbrace{6 + 6}^{2} + }{10}\\ \amp = \frac{ 2\cdot 2 + 3\cdot 1 + 4\cdot 3 + 5\cdot 2 + 6\cdot 6 }{10}\\ \amp = 2 \cdot \frac{2}{10} + 3 \cdot \frac{1}{10} + 4 \cdot \frac{3}{10} + 5 \cdot \frac{2}{10} + 6 \cdot \frac{2}{10}\\ \amp = 2 \cdot P(2) + 3 \cdot P(3) + 4 \cdot P(4) + 5 \cdot P(5) + 6 \cdot P(6)\\ \amp = 4.1 \end{align*}
Remark 6.1.6. Interpretation of the Mean.

Suppose an experiment is repeated \(n\) times, and the measurements of the random variable \(X\) are labeled: \(x_1, x_2, \ldots, x_n\) then as \(n\) goes to infinity, we expect the average of all measurements, \(\overline{x}\text{,}\) to get closer and closer to \(\mu_X\text{:}\)

\begin{equation*} \text{as } n \to \infty \qquad \mu_X - \overline{x} \to 0. \end{equation*}

where

\begin{equation*} \overline{x} = \frac{x_1 + x_2 + \cdots + x_n}{n}. \end{equation*}

In other words, the mean of a random variable represents what we would expect the average value of all the measurements to be in the long run, i.e. if we do the experiment many times.

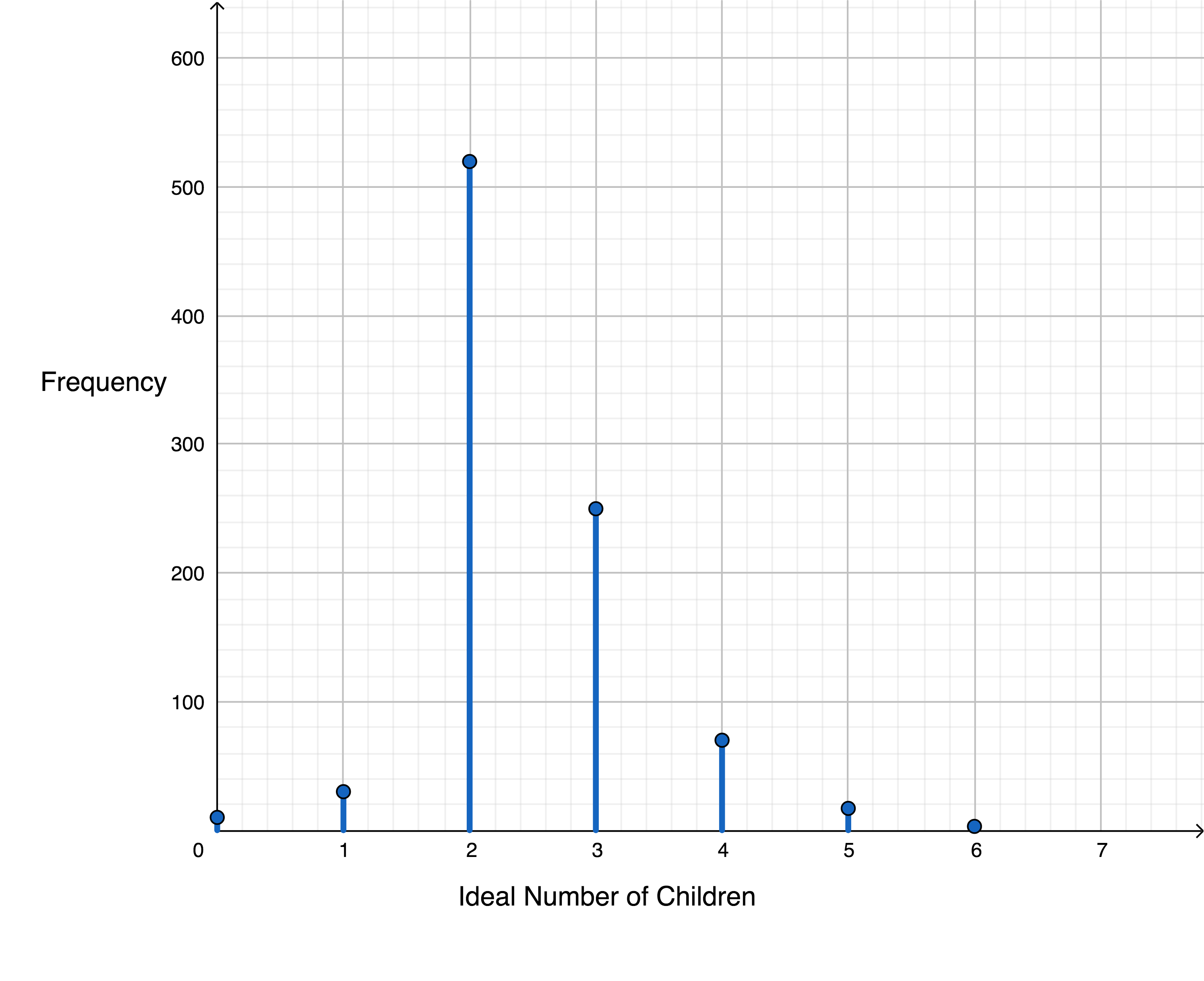
Reading Questions Ideal Number of Children

A random sample of 900 adult Americans were asked, “What is the ideal number of children to have in a family?”

\(x\) frequency
0 10
1 30
2 520
3 250
4 70
5 17
6 3
Table 6.1.8. Ideal number of children (frequency distribution)
Question 6.1.9.

Construct a discrete probability distribution for the variable \(X\text{.}\)

Solution
\(x\) \(P(x)\)
0 \(0.0\overline{1}\)
1 \(0.0\overline{3}\)
2 \(0.5\overline{7}\)
3 \(0.2\overline{7}\)
4 \(0.0\overline{7}\)
5 \(0.01\overline{8}\)
6 \(0.00\overline{3}\)
Table 6.1.10. Ideal number of children (probability distribution)
Question 6.1.11.

Compute the mean, \(\mu_X\text{,}\) and standard deviation, \(\sigma_X\text{.}\)

Solution

Using the TI-84 Plus calculator we first put the data from the frequency distribution into lists 1 and 2 and then press: stat -> CALC -> 1-Var Stats. Next, choose list 1 for List and list 2 for FreqList. Finally, cursor to Calculate and press enter.

This yields: \(\mu_X = 2.4478\) and \(\sigma_X =0.8308\text{.}\)

Question 6.1.12.

Draw the stick-graph of the discrete probability distribution.

Solution
Question 6.1.13.

What is the probability that a randomly selected adult thinks the ideal number of children is 2?

Answer

57.8%

Reading Questions Expected Value of a Straight Bet in Roulette

In the game of Roulette, a player can place a $1 bet on the number 17. This is called a straight bet. Since the wheel has pockets numbered 1–36, 0, and 00, there is a 1/38 chance the ball will land on 17. If the ball lands on 17, the player will win $36 (36 times the value of the bet). Win or lose, the casino takes the player's $1 bet.

Event \(x\) \(P(x)\)
17 \(36-1\) \(1/38\)
not 17 \(-1\) \(37/38\)
Table 6.1.14. Probability distribution for $1 bet

1.

What is the expected value of the game for the player?

Solution
\begin{align*} E[X] \amp = \mu_X\\ \amp = \sum x\cdot P(x)\\ \amp = (36-1)\cdot \frac{1}{38} + (-1)\frac{37}{38}\\ \amp = -0.05263 \end{align*}

Thus the player expects to lose more than $0.05 per spin.

2.

If you played 1000 times, how much would you expect to win or lose?

Solution
\begin{equation*} 1000\cdot E[X] = (1000)(-0.05263) = $52.63 \end{equation*}

Reading Questions Expected Value of a Term Life Insurance Policy

An insurance company sells a $250,000, 1-year term life insurance policy to a 20 year old female for $200. Accoring to the National Vital Statistics Report the probability that a 20 year old female survives the year is 0.999544. Compute and interpret the expected vale of this policy to the insurance company.

Event \(x\) \(P(x)\)
dies \(-250,000+200\) \(1-0.999544\)
does not die \(200\) \(0.999544\)
Table 6.1.15. Probability distribution for life insurance policy

1.

What is the expected value of the policy for the insurance company?

Solution
\begin{align*} E[X] \amp = \mu_X\\ \amp = \sum x\cdot P(x)\\ \amp = -249,800(0.000456) + 200(0.999544)\\ \amp = 86 \end{align*}

Thus the insurance company expects to earn $86 from the sale of the policy.

login